This virtual lab on 2D Matrices in Python is designed for undergraduate students. It aims to simplify the understanding of two-dimensional arrays by combining theory, visual aids, and interactive coding tools. The lab offers hands-on practice with matrix operations such as creation, traversal, and manipulation. By providing quizzes and step-by-step visualizations, it helps learners strengthen both conceptual clarity and problem-solving skills. This virtual setup ensures accessible, self-paced learning, especially for those without access to physical lab resources.
Aim
Theory & Applications
A matrix is a structured rectangular array comprising numbers, symbols, or expressions organized into rows
and columns.
Matrices are foundational in subjects like mathematics, computer science, engineering, physics, and data
science.
A 2D matrix (two-dimensional matrix) is a grid of elements arranged in horizontal rows and vertical columns.
Each element is identified by its position, given by a specific row and column index.
For example:
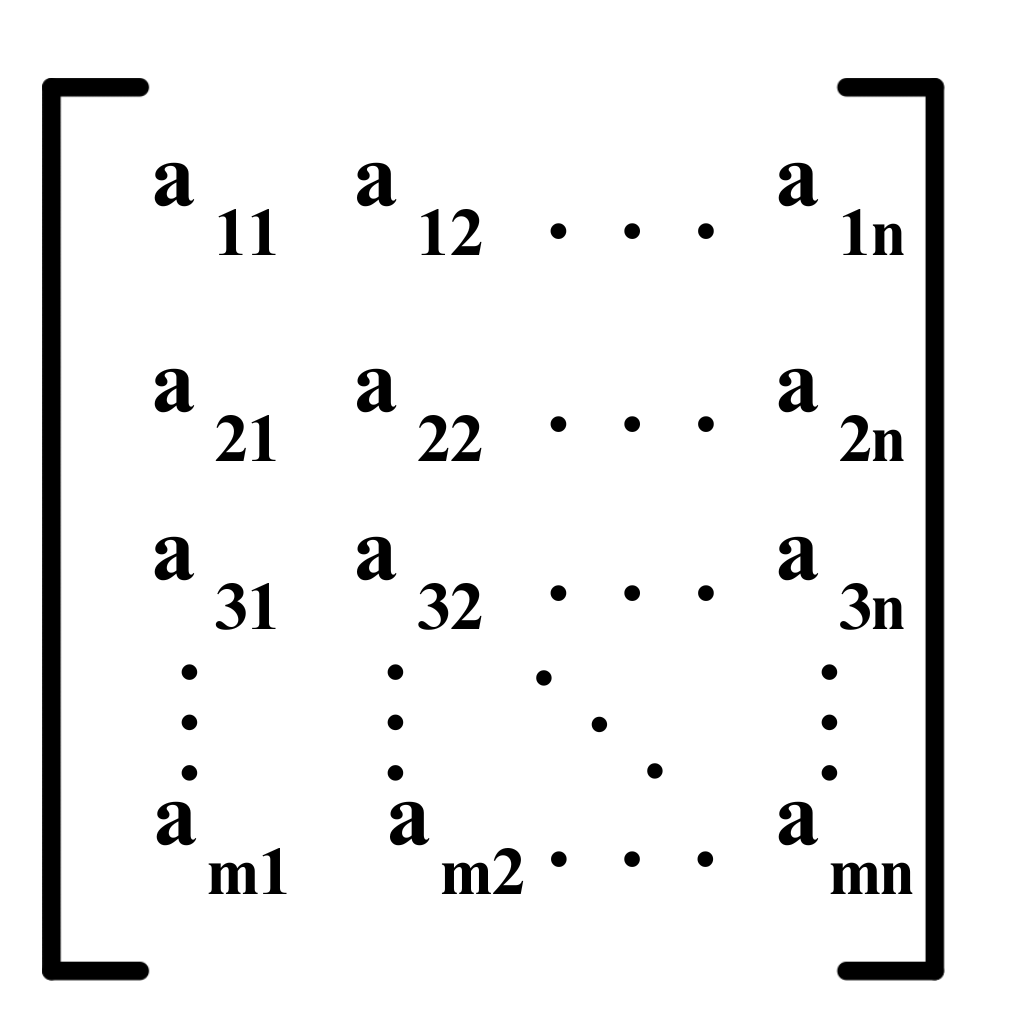A = [[1 2 3]
[4 5 6]
[7 8 9]]
- Rows→ Horizontal lines (e.g., [1, 2, 3] is the first row)
- Columns → Vertical lines (e.g., [1, 4, 7] is the first column)
- Elements: Individual values in the matrix (e.g., 5 is located at row 2, column 2)
- Square Matrix : Same number of rows and columns (e.g., 3×3)
- Rectangular Matrix : Different number of rows and columns (e.g., 2×4)
- Identity Matrix : Diagonal elements are 1; all other elements are 0
- Zero Matrix : All elements are 0
- Sparse Matrix : Contains mostly zeroes
2D matrices play a crucial role across various domains:
- Computer Graphics : Used for image rendering, transformations, and geometric modeling.
- Scientific Computing : Essential for solving complex simulations and mathematical computations in physics and engineering.
- Machine Learning & Data Science : Represent datasets, perform matrix operations, and power neural networks.
- Cryptography : Employed in encoding and decoding algorithms to secure information.
- Game Development : Used in pathfinding, map grids, and collision detection.
- Network Theory : Represent graphs and connections using adjacency matrices.
- Understand the concept of a 2D matrix
- Understanding its applications.
- Implement a 2D matrix generation algorithm using Python (with optional C/Java versions).
- Visualize the matrix
- Practice questions for the conceptual study of matrix
- Develop an interactive virtual lab experience for users.
Procedure
Step 1 – Create the Matrix:
- Name the function
create_matrix(m, n), where: mis the number of rowsnis the number of columns- Ask the user to enter
m × nvalues one by one - Return the created matrix
Step 2 – Traverse the Matrix:
- Name the function
traverse_matrix(matrix, r, c), where: matrixis the matrix to traverseris the row indexcis the column index- Check if the index is valid by comparing
randcwith matrix dimensions - If valid, print the value at
matrix[r][c] - If invalid, print
"Invalid index!"
Step 3 – Manipulate the Matrix:
- Name the function
manipulate_matrix(matrix, r, c, new_value), where: matrixis the matrix to manipulateris the row indexcis the column indexnew_valueis the new value to assign- Check if the index is valid
- If valid, update
matrix[r][c]withnew_valueand print a confirmation message - If invalid, print
"Invalid index!"
Final Output:
- First, display the entire matrix after creation
- Then, traverse and display the value at the specified index
- Next, manipulate the matrix and show the updated matrix
Code
Example programs
// C++ Code Example
#include <iostream>
#include <vector>
using namespace std;
// Step 1: Create the matrix
vector<vector<int>> createMatrix(int m, int n) {
vector<vector<int>> matrix(m, vector<int>(n));
cout << "Enter " << m * n << " elements one by one:" << endl;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> matrix[i][j];
}
}
return matrix;
}
// Step 2: Traverse the matrix by index
void traverseMatrix(const vector<vector<int>>& matrix, int r, int c) {
if (r < 0 || r >= matrix.size() || c < 0 || c >= matrix[0].size()) {
cout << "Invalid index!" << endl;
} else {
cout << "Value at index [" << r << "][" << c << "] is " << matrix[r][c] << endl;
}
}
// Step 3: Manipulate the matrix at a given index
void manipulateMatrix(vector<vector<int>>& matrix, int r, int c, int newValue) {
if (r < 0 || r >= matrix.size() || c < 0 || c >= matrix[0].size()) {
cout << "Invalid index!" << endl;
} else {
matrix[r][c] = newValue;
cout << "Updated value at index [" << r << "][" << c << "] to " << newValue << endl;
}
}
int main() {
int m, n;
cout << "Enter number of rows: ";
cin >> m;
cout << "Enter number of columns: ";
cin >> n;
vector<vector<int>> mat = createMatrix(m, n);
cout << "\nMatrix:" << endl;
for (const auto& row : mat) {
for (int val : row) {
cout << val << " ";
}
cout << endl;
}
// Traversal
int r, c;
cout << "\nEnter row index to traverse: ";
cin >> r;
cout << "Enter column index to traverse: ";
cin >> c;
traverseMatrix(mat, r, c);
// Manipulation
cout << "\nEnter row index to update: ";
cin >> r;
cout << "Enter column index to update: ";
cin >> c;
int newValue;
cout << "Enter new value: ";
cin >> newValue;
manipulateMatrix(mat, r, c, newValue);
cout << "\nUpdated Matrix:" << endl;
for (const auto& row : mat) {
for (int val : row) {
cout << val << " ";
}
cout << endl;
}
return 0;
}
# Python Code Example
# Step 1: Create the matrix
def create_matrix(m,n):
if len(elements) < m * n:
print("insufficient elements to populate the matrix!")
return None
M = []
for i in range(m):
row = []
for j in range(n):
val = input(f"Element at ({i+1},{j+1}): ")
row.append(val)
M.append(row)
return M
# Step 2: Traverse the matrix by index
def traverse_matrix(matrix, r, c):
if r < 0 or r >= len(matrix) or c < 0 or c >= len(matrix[0]):
print("Invalid index!")
else:
print(f"Value at index [{r}][{c}] is {matrix[r][c]}")
# Step 3: Manipulate the matrix at a given index
def manipulate_matrix(matrix, r, c, new_value):
if r < 0 or r >= len(matrix) or c < 0 or c >= len(matrix[0]):
print("Invalid index!")
else:
matrix[r][c] = new_value
print(f"Updated value at index [{r}][{c}] to {new_value}")
# Example usage:
m = int(input("Enter number of rows: "))
n = int(input("Enter number of columns: "))
mat = create_matrix(m, n)
print("\nMatrix:")
for row in mat:
print(row)
# Traversal
r = int(input("\nEnter row index to traverse: "))
c = int(input("Enter column index to traverse: "))
traverse_matrix(mat, r, c)
# Manipulation
r = int(input("\nEnter row index to manipulate: "))
c = int(input("Enter column index to manipulate: "))
new_value = int(input("Enter new value: "))
manipulate_matrix(mat, r, c, new_value)
print("\nUpdated Matrix:")
for row in mat:
print(row)
Matrix Learning Journey
Welcome! In this lab, we will learn matrices step by step:
1. Creation → 2. Traversal → 3. Manipulation
Result
This virtual lab provides hands-on experience with 2D matrix generation using various techniques. It enables users to explore different methods, implement code in multiple languages, and visualize the results for better comprehension. Comprehending 2D matrices is crucial for domains like numerical computing, cryptography, and machine learning.
Quiz
References
-
Python Matrix Basics
- Python Lists - W3Schools
- Matrix Applications - Linear Algebra
Team & Tools
Students
Mentor
- Ms. Shiva Saini
Tools Used
- Vanilla HTML, CSS, JS - for creating the web page